Dynamic Balancing, From Theory to Reality
I built a self-balancing robot using an IMU, DC motors, and custom C code. The goal: design a system that mimics how a human balances on a Segway, by constantly adjusting its position using sensor feedback and control theory.

The Challenge
Understanding system dynamics
To create a self-balancing Segway, we had to first understand the physics of inverted pendulums, system dynamics, and how to maintain stability in an unstable system.
Combining software with hardware
A major challenge was fusing real-time sensor data from the IMU with software control algorithms to drive motors fast enough to correct balance before falling.
Ensuring responsive real-time control
Designing an embedded system that reacts with minimal delay required careful interrupt handling, tuning of the PID controller, and low-latency code on the Bela platform.
Our Solution
We developed a fully working self-balancing two-wheel robot using brushless motors, an IMU, and a custom PID controller. The project was split into modular stages—signal reading, system modelling, controller design, and motor integration—culminating in a real-time feedback loop that allows the Segway to maintain upright position autonomously.
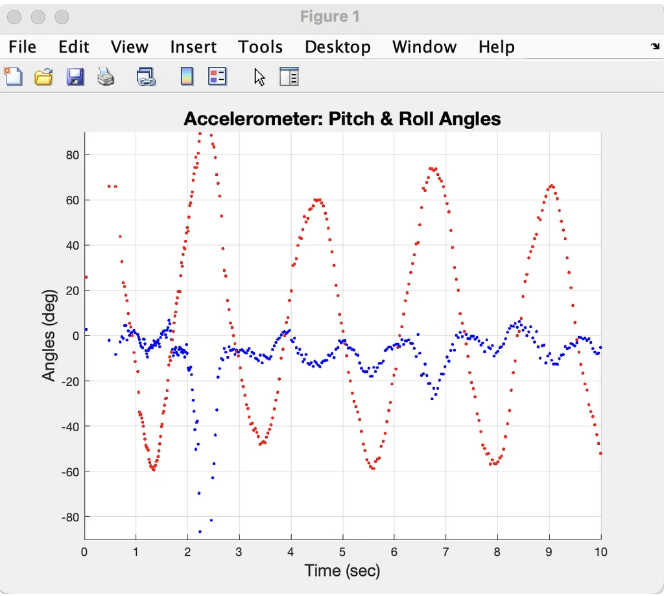
Sensor Fusion with IMU
We used a 6-axis inertial measurement unit (MPU6050) to read pitch angle and angular velocity in real time, filtered using a complementary filter.
Real-Time Control with PID
A custom-tuned PID controller calculates the corrective motor torque required to maintain balance based on the current angle error and angular velocity.
Motor Control with PWM
Two high-torque DC motors are driven via PWM signals and H-bridges, ensuring smooth bidirectional motion and fast response to PID commands.
Characterising System Response
We used step response testing and transfer function estimation from Lab 3 to model the Segway as a second-order system, allowing accurate controller tuning and simulation.
Key Impact
- Real-time system modeling and feedback loop
- Accurate angle sensing and filtering
- Stable upright balancing for small disturbances
- Hands-on application of control theory
- Bridging control theory and physical system design
- Applied embedded systems and low-level programming